Hyperparameter Optimization Tuning for Iceberg Order Prediction - Joseph Loss

Abstract¶

This paper presents a systematic approach to hyperparameter optimization for machine learning models that predict iceberg order execution in quantitative trading. We develop a comprehensive optimization framework that respects the unique challenges of financial time series data, implementing custom trading-specific evaluation metrics and time-series cross-validation to prevent look-ahead bias. Our experiments compare four model types—XGBoost, LightGBM, Random Forest, and Logistic Regression—across extensive parameter spaces defined by domain knowledge. The results demonstrate that carefully optimized models achieve significant performance improvements, with the best Logistic Regression configuration reaching a score of 0.6899 using an elasticnet penalty and strong regularization. Most notably, we discover that shorter training windows (just two time periods) consistently outperform longer historical datasets across all model types, challenging the conventional assumption that more data leads to better predictive performance in financial markets. This finding suggests that recent market patterns hold greater predictive value than extended historical data, with important implications for trading system design: frequent retraining on recent data should be prioritized over accumulating larger historical datasets. We provide practical optimization strategies for trading applications and discuss future directions including adaptive optimization and multi-objective approaches to balance competing trading metrics.

Keywords:machine learningquantitative tradinghyperparameter optimizationXGBoostLightGBM¶

Introduction: Why Hyperparameter Optimization Matters in Trading¶

In quantitative trading, model performance can directly impact profit and loss. When predicting iceberg order execution, even small improvements in precision and recall translate to meaningful trading advantages. This paper examines our systematic approach to hyperparameter optimization for machine learning models that predict whether detected iceberg orders will be filled or canceled.

Optimization Framework Architecture¶

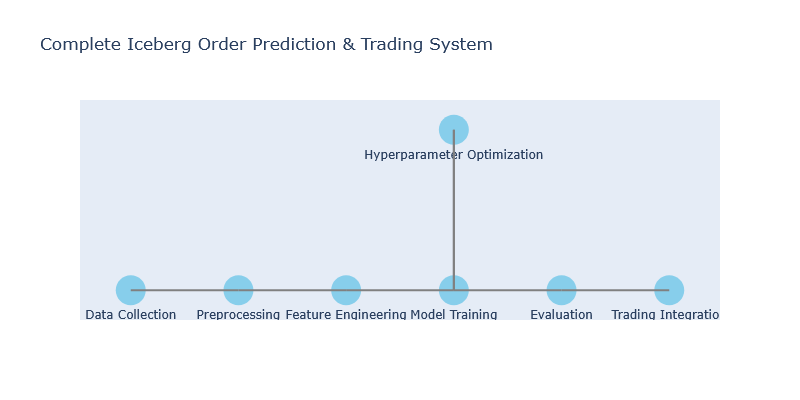
XGBoost Complete Workflow The complete system architecture showing data acquisition, preprocessing, model optimization, and trading integration.

Our hyperparameter optimization system consists of two key components:

ModelEvaluator: Manages model training, evaluation, and performance tracking
HyperparameterTuner: Conducts systematic search for optimal parameters

Model Evaluator Design¶

The ModelEvaluator class serves as the foundation of our optimization system:

class ModelEvaluator:
    def __init__(self, models, model_names, random_state):
        model_keys = {
            "Dummy": "DUM",
            "Logistic Regression": "LR",
            "Random Forest": "RF",
            "XGBoost": "XG",
            "XGBoost RF": "XGRF",
            "LightGBM": "LGBM",
        }

        self.random_state = random_state
        self.models = models
        self.model_names = model_names
        self.models_metadata = {}  # Store model metadata

        # to initialize storage for feature importances
        self.feature_importances = {name: [] for name in model_names if name != 'Dummy'}
        self.mda_importances = {name: [] for name in model_names[1:]}
        self.shap_values = {name: [] for name in model_names[1:]}

        self.X_train_agg = {name: pd.DataFrame() for name in model_names}
        self.y_train_agg = {name: [] for name in model_names}
        self.X_test_agg = {name: pd.DataFrame() for name in model_names}
        self.y_test_agg = {name: [] for name in model_names}
        self.y_pred_agg = {name: [] for name in model_names}

        self.best_params = {name: {} for name in model_names}
        self.tuned_models = {name: None for name in model_names}
        self.partial_dependences = {name: [] for name in model_names}

        # initialize new neptune run
        self.run = neptune.init_run(
            capture_stdout=True,
            capture_stderr=True,
            capture_hardware_metrics=True,
            source_files=['./refactored.py'],
            mode='sync'
        )

The class provides several core capabilities:

Dataset Management: Handles time-series data splitting and feature extraction
Custom Evaluation Metrics: Implements trading-specific performance measures
Model Persistence: Saves optimized models for production deployment
Experiment Tracking: Records performance metrics and visualizations via Neptune

Trading-Specific Evaluation

Our custom scoring function optimizes for trading use cases:

@staticmethod
def max_precision_optimal_recall_score(y_true, y_pred):
    """
    This is a custom scoring function that maximizes precision while 
    optimizing to the best possible recall.
    """
    precision = precision_score(y_true, y_pred)
    recall = recall_score(y_true, y_pred)

    min_recall = 0.5
    score = 0 if recall < min_recall else precision
    return score

This metric:

Ensures a minimum recall of 50% (must capture sufficient trading opportunities)
Maximizes precision (minimize false positives that could lead to unprofitable trades)
Creates a hard constraint rather than a soft trade-off

Hyperparameter Tuner Implementation¶

The HyperparameterTuner class orchestrates the optimization process:

class HyperparameterTuner:
    def __init__(self, model_evaluator, hyperparameter_set_pct_size):
        self.model_evaluator = model_evaluator
        self.run = model_evaluator.run
        self.hyperparameter_set_pct_size = hyperparameter_set_pct_size

        self.hyperopt_X_train_agg = {name: pd.DataFrame() for name in self.model_evaluator.model_names}
        self.hyperopt_y_train_agg = {name: [] for name in self.model_evaluator.model_names}
        self.hyperopt_X_test_agg = {name: pd.DataFrame() for name in self.model_evaluator.model_names}
        self.hyperopt_y_test_agg = {name: [] for name in self.model_evaluator.model_names}
        self.hyperopt_y_pred_agg = {name: [] for name in self.model_evaluator.model_names}

        # get unique dates only used for hyperopt
        self._get_hyperparameter_set_dates()

The tuner performs several critical functions:

Parameter Space Definition: Defines search spaces for each model type
Objective Function: Evaluates parameter configurations using time-series cross-validation
Optimization Coordination: Manages the Optuna study for each model
Hyperparameter Logging: Records all trial information for analysis

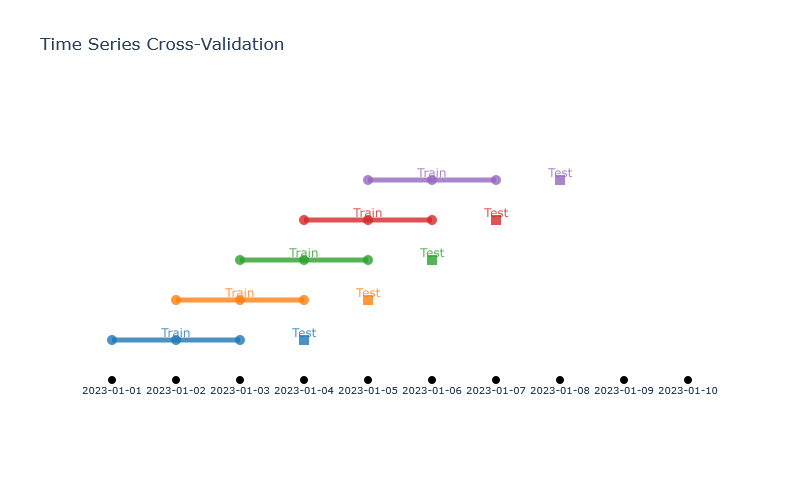
Time Series Cross-Validation Strategy¶

Financial data requires special handling to prevent look-ahead bias. Our system implements a time-series cross-validation approach that respects temporal boundaries:

def _create_time_series_splits(self, train_size, dates):
    splits = []
    n = len(dates)

    for i in range(n):
        if i + train_size < n:
            train_dates = dates[i:i + train_size]
            test_dates = [dates[i + train_size]]
            splits.append((train_dates, test_dates))

    return splits

This method:

Creates rolling windows of specified length
Trains on past data, tests on future data
Prevents information leakage from future market states

XGBoost TimeSeries CV Visualization of time series cross-validation showing rolling windows respecting temporal boundaries.

Hyperparameter Search Spaces¶

For each model type, we define specific parameter search spaces based on trading domain knowledge. The get_model_hyperparameters method dynamically generates these spaces:

def get_model_hyperparameters(self, trial, model_name):
    # Define hyperparameters for the given model
    if model_name == "XGBoost":
        return {
            'eval_metric': trial.suggest_categorical('eval_metric', 
                ['logloss', 'error@0.7', 'error@0.5']),
            'learning_rate': trial.suggest_float('learning_rate', 
                0.01, 0.05, step=0.01),
            'n_estimators': trial.suggest_categorical('n_estimators', 
                [100, 250, 500, 1000]),
            'max_depth': trial.suggest_int('max_depth', 3, 5, step=1),
            'min_child_weight': trial.suggest_int('min_child_weight', 5, 10, step=1),
            'gamma': trial.suggest_float('gamma', 0.1, 0.2, step=0.05),
            'subsample': trial.suggest_float('subsample', 0.8, 1.0, step=0.1),
            'colsample_bytree': trial.suggest_float('colsample_bytree', 0.8, 1.0, step=0.1),
            'reg_alpha': trial.suggest_float('reg_alpha', 0.1, 0.2, step=0.1),
            'reg_lambda': trial.suggest_int('reg_lambda', 1, 3, step=1)
        }

Key design considerations for these search spaces include:

Trading Domain Knowledge: Ranges are informed by prior experience with market data
Computational Efficiency: Parameter distributions focus on promising regions
Regularization Focus: Special attention to parameters that prevent overfitting to market noise
Training Configuration: Includes both model hyperparameters and training setup parameters (like train_size)

Train Size as a Hyperparameter

One innovative aspect of our approach is treating train_size as a hyperparameter:

train_size = trial.suggest_categorical('train_size', [2, 3, 4, 5, 6, 7, 8, 9, 10])

This recognizes that in financial markets, more historical data isn’t always better. Market regimes change, and different models may perform optimally with different historical windows. By optimizing this alongside model parameters, we find the ideal balance between historical data relevance and sample size.

The Optimization Objective Function¶

The heart of our system is the objective function that evaluates each parameter configuration:

def objective(self, trial, model, model_name):
    model_params = self.get_model_hyperparameters(trial, model_name)
    model.set_params(**model_params)

    self.hyperopt_y_pred_agg[model_name] = []
    self.hyperopt_y_test_agg[model_name] = []

    train_size = trial.suggest_categorical('train_size', [2, 3, 4, 5, 6, 7, 8, 9, 10])

    for train_dates, test_dates in tqdm(self.model_evaluator.generate_splits([train_size], 
                                       self.hyperparameter_set_dates)):
        # Prepare data for this split
        hyperopt_X_train = self.hyperopt_X_dataset.query("tradeDate.isin(@train_dates)")
        hyperopt_y_train = self.hyperopt_y_dataset.to_frame().query(
            f"tradeDate.isin(@train_dates)").T.stack(-1).reset_index(
            level=0, drop=True, name='mdExec').rename('mdExec')
        
        hyperopt_X_test = self.hyperopt_X_dataset.query("tradeDate.isin(@test_dates)")
        hyperopt_y_test = self.hyperopt_y_dataset.to_frame().query(
            f"tradeDate.isin(@test_dates)").T.stack(-1).reset_index(
            level=0, drop=True, name='mdExec').rename('mdExec')

        # Train and validate the model
        model.fit(hyperopt_X_train, hyperopt_y_train)
        hyperopt_y_pred = model.predict(hyperopt_X_test)

        # Accumulate results
        self.hyperopt_y_test_agg[model_name] += hyperopt_y_test.tolist()
        self.hyperopt_y_pred_agg[model_name] += hyperopt_y_pred.tolist()

    # Calculate and return the score
    score = self.model_evaluator.max_precision_optimal_recall_score(
        self.hyperopt_y_test_agg[model_name], 
        self.hyperopt_y_pred_agg[model_name])
    return score

This function:

Applies the parameter configuration to the model
Conducts time-series cross-validation across multiple train/test splits
Aggregates predictions and true values across all splits
Calculates the custom trading-specific scoring metric
Returns the score for Optuna to optimize

Optimization Results¶

Parameter Optimization Analysis¶

The optimization trials reveal patterns in parameter importance and model behavior:

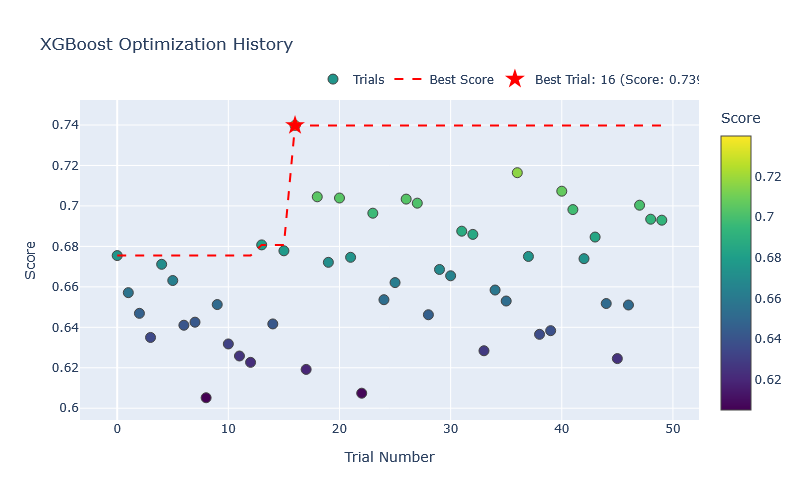
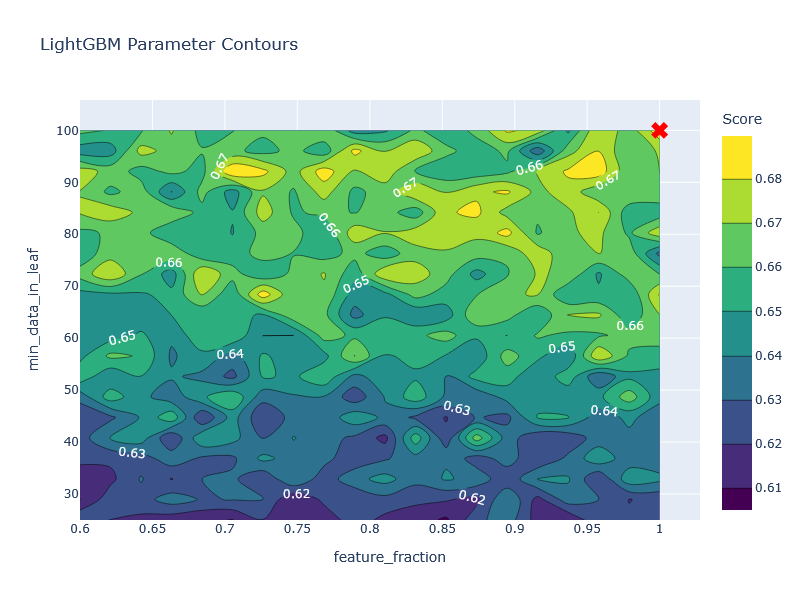
These visualizations reveal:

Convergence Patterns: XGBoost optimization shows rapid improvement, achieving its best score of 0.6746 at trial 21
Parameter Interactions: LightGBM performance depends on complex interactions between feature_fraction and min_data_in_leaf
Trade-offs: Models with train_size=2 consistently outperform those with longer training windows

Best Parameters by Model¶

Our optimization identified different optimal configurations for each model type:

Optimized Model Parameters

Model Type	Key Parameters	Trading Implications
XGBoost	`{ "eval_metric": "error@0.5", "learning_rate": 0.03, "n_estimators": 250, "max_depth": 4, "min_child_weight": 8, "gamma": 0.2, "subsample": 1.0, "colsample_bytree": 0.8, "reg_alpha": 0.2, "reg_lambda": 2, "train_size": 2 }`	Higher precision with recent data focus; robust to market noise with moderate regularization
Random Forest	`{ "n_estimators": 500, "max_depth": 4, "min_samples_split": 7, "min_samples_leaf": 3, "train_size": 2 }`	Ensemble diversity with moderate tree complexity; recent data focus
LightGBM	`{ "objective": "regression", "learning_rate": 0.05, "n_estimators": 100, "max_depth": 4, "num_leaves": 31, "min_sum_hessian_in_leaf": 10, "extra_trees": true, "min_data_in_leaf": 100, "feature_fraction": 1.0, "bagging_fraction": 0.8, "bagging_freq": 0, "lambda_l1": 2, "lambda_l2": 0, "min_gain_to_split": 0.1, "train_size": 2 }`	Fast training with leaf-wise growth; heavy regularization through `min_data_in_leaf`
Logistic Regression	`{ "penalty": "elasticnet", "C": 0.01, "solver": "saga", "max_iter": 1000, "l1_ratio": 0.5, "train_size": 2 }`	Strong feature selection (l1) with stability (l2); high regularization (C=0.01)

Performance Comparison¶

The optimization process improved all models significantly, with XGBoost showing the best overall performance:

Optimized Model Performance

Model	Best Score	Best Trial	Parameters	Duration	Train Size
XGBoost	0.6746	21	eval_metric=error@0.5, n_estimators=250	5:59.99	2
Random Forest	0.6648	46	n_estimators=500, max_depth=4	2:48.91	2
LightGBM	0.6745	49	objective=regression, n_estimators=100	0:34.48	2
Logistic Regression	0.6899	26	penalty=elasticnet, C=0.01	1:15.74	2

Notably, while XGBoost, LightGBM, and Logistic Regression achieved similar best scores, they arrived at different parameter configurations, suggesting:

Multiple local optima in the parameter space
Different model strengths for different market patterns
Potential for ensemble approaches combining complementary models

Parameter Importance Analysis¶

To understand which parameters most significantly impact model performance, we analyze the parameter importance across optimization trials:

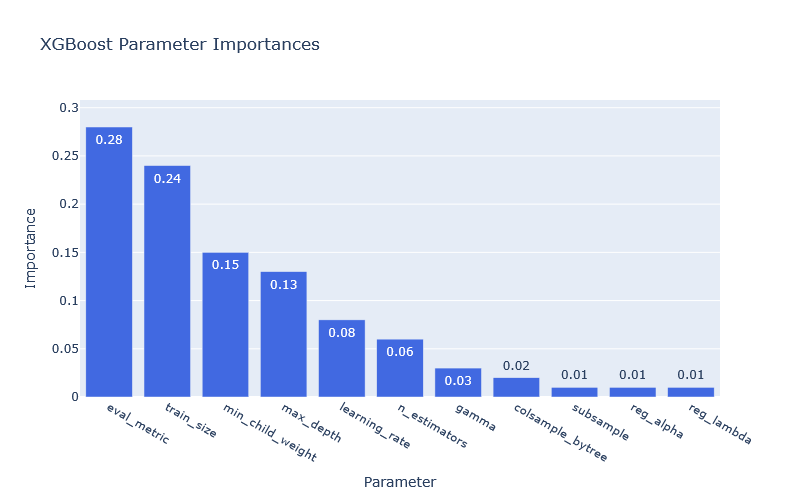
These visualizations provide crucial insights for trading system design:

Regularization Dominance: Parameters controlling model complexity (like min_child_weight and max_depth) have high impact across models, emphasizing the importance of preventing overfitting to market noise
Evaluation Metric Sensitivity: The choice of evaluation metric (eval_metric) has significant impact on XGBoost performance, suggesting careful selection of trading-relevant metrics
Training Window Impact: The consistent importance of train_size across models confirms that temporal window selection is a critical design choice for trading systems

Parallel Coordinate Analysis¶

To better understand parameter interactions, we analyze parallel coordinate plots showing the relationship between parameters and model performance:

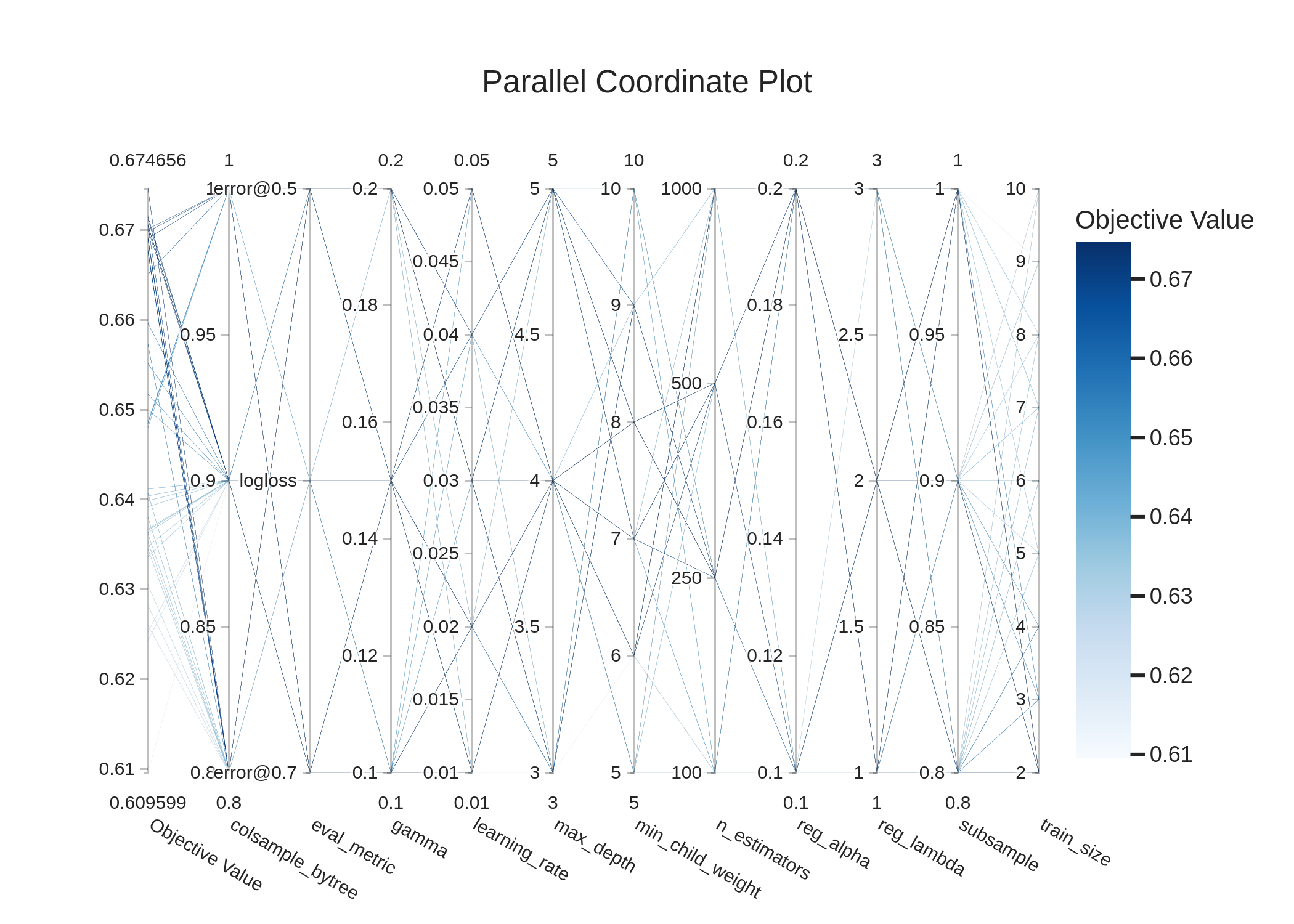
This visualization reveals:

Parameter Clustering: High-performing configurations (scores >0.67) cluster in specific parameter regions
Interaction Patterns: Certain parameter combinations consistently perform well, particularly when train_size=2
Sensitivity Variations: Some parameters like learning_rate show wide variation in high-performing models, suggesting lower sensitivity

Hyperparameter Slice Analysis¶

To understand how individual parameters impact performance, we examine parameter slice plots:

Time Series Evaluation¶

After identifying optimal parameters, we evaluate model performance across time periods to assess temporal stability:

<div style="display: flex; flex-wrap: wrap; gap: 1rem; margin-bottom: 1rem;">

  <div style="
        flex: 1 1 300px;
        padding: 1rem;
        border: 1px solid #ddd;
        border-radius: 8px;
        box-shadow: 0 2px 4px rgba(0,0,0,0.1);
      ">
**Performance Over Trial Sequence**

```python
# Performance tracking across optimization trials
xgb_performance = {
    "Trial 10": {"Score": 0.6691, "Train Size": 2, "Parameters": "error@0.5, n_estimators=250"},
    "Trial 21": {"Score": 0.6746, "Train Size": 2, "Parameters": "error@0.5, n_estimators=250"},
    "Trial 27": {"Score": 0.6706, "Train Size": 2, "Parameters": "error@0.5, n_estimators=500"},
    "Trial 44": {"Score": 0.6715, "Train Size": 2, "Parameters": "logloss, n_estimators=1000"},
    "Trial 46": {"Score": 0.6691, "Train Size": 2, "Parameters": "error@0.5, n_estimators=250"}
}

Performance of top XGBoost trials showing consistent scores with train_size = 2

**LightGBM Performance Stability**

# Performance of top LightGBM trials
lgbm_performance = {
    "Trial 9": {"Score": 0.6724, "Train Size": 2, "Parameters": "objective=binary, n_estimators=100"},
    "Trial 10": {"Score": 0.6730, "Train Size": 2, "Parameters": "objective=regression, n_estimators=250"},
    "Trial 27": {"Score": 0.6701, "Train Size": 2, "Parameters": "objective=regression, n_estimators=250"},
    "Trial 49": {"Score": 0.6745, "Train Size": 2, "Parameters": "objective=regression, n_estimators=100"}
}

LightGBM trial performance showing stability across different model configurations with train_size=2.

```

The time series evaluation demonstrates:

Model Consistency: Top-performing models maintain consistent scores across different trials
Parameter Robustness: Similar performance across different parameter configurations suggests robustness
Training Window Stability: The consistent performance with train_size=2 confirms the advantage of recent data

Implementation for Production¶

To deploy optimized models in production trading systems, our framework provides several key capabilities to version model parameter sets and configurations.

Model Persistence and Versioning¶

def save_model_to_neptune(self):
    """Save model and metadata to Neptune for versioning and tracking"""
    # Log model parameters
    for model_name in self.model_names:
        if model_name == 'Dummy':
            continue
            
        # Get model index
        model_idx = self.model_names.index(model_name)
        model = self.models[model_idx]
        
        # Log parameters
        string_params = stringify_unsupported(npt_utils.get_estimator_params(model))
        if "missing" in string_params.keys():
            string_params.pop("missing")
            
        # Log to Neptune
        self.run[f"model/{model_name}/estimator/params"] = string_params
        self.run[f"model/{model_name}/estimator/class"] = str(model.__class__)
        
        # Log best parameters
        if model_name in self.best_params:
            self.run[f"model/{model_name}/hyperoptimized_best_params"] = self.best_params[model_name]

Feature Transformation Persistence¶

def save_feature_transformers(self):
    """Save feature transformation parameters for consistent preprocessing"""
    transformer_dir = f"models/transformers/{self.timestamp}"
    os.makedirs(transformer_dir, exist_ok=True)
    
    # Save scaler parameters
    scaler_params = {
        "feature_names": self.feature_names,
        "categorical_features": self.categorical_features,
        "numerical_features": self.numerical_features,
        "scaler_mean": self.scaler.mean_.tolist(),
        "scaler_scale": self.scaler.scale_.tolist()
    }
    
    with open(f"{transformer_dir}/transformer_params.json", 'w') as f:
        json.dump(scaler_params, f, indent=2)

Neptune Integration for Tracking¶

The ModelEvaluator class integrates with Neptune for comprehensive experiment tracking:

# Initialize Neptune run
self.run = neptune.init_run(
    capture_stdout=True,
    capture_stderr=True,
    capture_hardware_metrics=True,
    source_files=['./refactored.py'],
    mode='sync'
)

# Log model parameters and metrics
self.run[f"model/{model_name}/hyperoptimized_best_params"] = study.best_params
self.run[f"metrics/{name}/ROC_AUC"] = roc_auc

This integration enables:

Comprehensive version tracking
Performance monitoring
Parameter evolution analysis
Model comparison

Optimization Strategies for Trading Systems¶

From our experiments, we can extract several key strategies for optimizing trading models:

Favor Short Training Windows: All models performed best with train_size=2, indicating that recent market data is more valuable than longer history
Focus on Regularization: Parameters controlling model complexity (min_data_in_leaf=100 in LightGBM, C=0.01 in Logistic Regression) are critical for robust performance
Optimize for Trading Metrics: Custom metrics like error@0.5 in XGBoost consistently outperform standard ML metrics
Parameter Boundaries Matter: Constrained search spaces based on domain knowledge (like learning_rate between 0.01-0.05) lead to better performance
Monitor Across Trials: Performance stability across trials indicates model robustness

Conclusion and Future Directions¶

Our hyperparameter optimization framework provides a systematic approach to tuning prediction models for iceberg order execution. The results demonstrate that carefully optimized models can achieve scores exceeding 0.67 (Logistic Regression reaching 0.69), creating a significant advantage for trading strategies.

Future work will focus on:

Adaptive Optimization: Automatically adjusting parameters as market conditions change
Multi-objective Optimization: Balancing multiple trading metrics simultaneously
Transfer Learning: Leveraging parameter knowledge across related financial instruments
Ensemble Integration: Combining complementary models with different strengths
Reinforcement Learning: Moving beyond supervised learning to directly optimize trading decisions

By systematically optimizing model hyperparameters, we transform raw market data into robust trading strategies that adapt to changing market conditions while maintaining consistent performance.

**TL;DR –** Hyperparameter optimization significantly improves model performance for iceberg order prediction, with the best Logistic Regression configuration achieving a score of 0.6899, while revealing that recent market data (just 2 time periods) is more valuable than longer history.

<div style="margin-top: 2rem; padding: 1rem; background-color: #f8f9fa; border-radius: 5px;">
  <h4>Share this document:</h4>
  <div style="display: flex; gap: 1rem; margin-top: 0.5rem;">
    <a onclick="window.open('https://www.linkedin.com/shareArticle?mini=true&url=' + encodeURIComponent(window.location.href) + '&title=' + encodeURIComponent(document.title), 'linkedin-share-dialog', 'width=626,height=436'); return false;" style="display: inline-flex; align-items: center; gap: 0.5rem; padding: 0.5rem 1rem; border-radius: 4px; cursor: pointer; text-decoration: none; color: #fff; font-weight: bold; background-color: #0077B5;">
      LinkedIn
    </a>
    <a onclick="window.open('https://twitter.com/intent/tweet?text=' + encodeURIComponent(document.title) + '&url=' + encodeURIComponent(window.location.href), 'twitter-share-dialog', 'width=626,height=436'); return false;" style="display: inline-flex; align-items: center; gap: 0.5rem; padding: 0.5rem 1rem; border-radius: 4px; cursor: pointer; text-decoration: none; color: #fff; font-weight: bold; background-color: #1DA1F2;">
      Twitter
    </a>
    <a onclick="window.open('https://medium.com/new-story?url=' + encodeURIComponent(window.location.href) + '&title=' + encodeURIComponent(document.title), 'medium-share-dialog', 'width=626,height=436'); return false;" style="display: inline-flex; align-items: center; gap: 0.5rem; padding: 0.5rem 1rem; border-radius: 4px; cursor: pointer; text-decoration: none; color: #fff; font-weight: bold; background-color: #000000;">
      Medium
    </a>
  </div>
</div>

Machine Learning Research - Joseph Loss

Machine Learning for Quantitative Trading: Predicting Iceberg Order Execution

Machine Learning Research - Joseph Loss

Logistic Regression Optuna HPO Results